Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning
0.写在前面
在这篇文章中,作者基于深度强化学习提出了一种新型的速度伺服系统控制策略,可以一定程度上解决速度伺服系统的控制参数在实际应用中难以调节且运行中易出现力矩扰动和惯量突变的问题。具体而言,作者探索了两种速度伺服系统控制策略,一种采用RL方法对PID控制参数进行整定,另一种采用RL方法自适应的对PID控制的电流进行补偿。实验结果表明,将传统的PID控制方法与RL方法进行结合能够有效的解决实际应用过程中面对力矩扰动和惯量突变等情况传统PID方法无法自适应的问题。
1. 论文基本信息
2. 论文主要内容
速度伺服系统模型分析
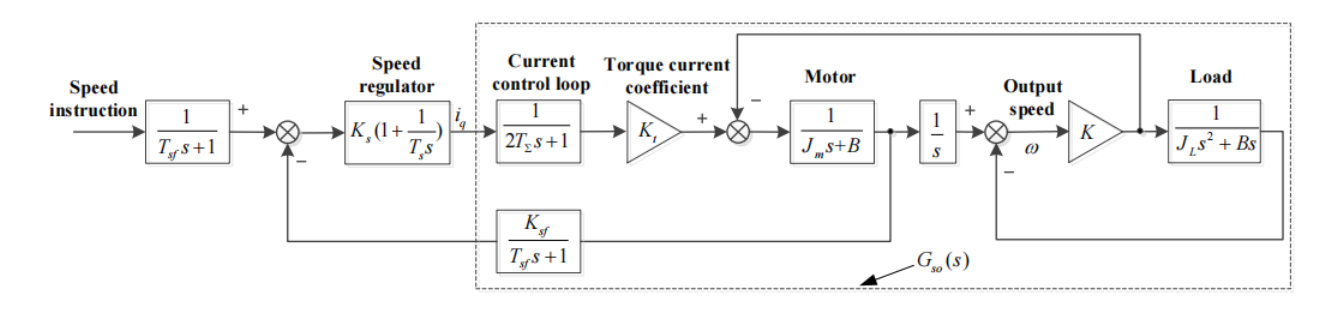
速度伺服系统由电流控制环、伺服电机、负载和反馈系统组成。根据速度环组成部分的分析,可将电流闭环、电机和速度检测假设为一阶系统,并采用PI控制算法作为速度调节器,可得到如图所示的速度伺服系统结构。
其中,Ks 是电流回路的比例增益,Ts 是积分时间常数,Kt 是伺服系统转矩电流系数。Ksf = 60 m / fp T 是速度反馈系数,m 是检测到的脉冲数,pf 代表编码器的分辨率,T 是速度检测周期。2TΣ 是电流回路近似系统的时间常数。Tsf 是速度反馈近似系统的时间常数,K 是机械传动的刚度系数,B 是负载摩擦力的换算系数。
关于伺服系统的建模推到过程可以具体参看论文原文,这里值得指出的是,负载转矩变化引起的速度波动与系统惯量和负载转矩都有关系。惯量越小,说明相同负载转矩波动对速度控制过程的影响越大。伺服系统运行时应仔细考虑系统惯量和负载扭矩,以获得稳定的速度响应。例如,机器人手臂在运动过程中,其惯性不断变化。因此在数控加工过程中,加工零件的质量会降低,从而导致进给轴的换算惯量发生变化。当负载对象的特性发生变化时,整个伺服系统的特性也会发生变化。如果系统惯量增大,系统的响应就会变慢,这很可能会导致系统不稳定并导致爬升。相反,如果系统惯性减小,动态响应就会加快,出现速度超调和扰动。
在这篇文章中,伺服系统的数学模型如下图所示,伺服系统在运行过程中的转动惯量和外部力矩扰动可视为是图中的系统1、2、3在不同时刻之间的跳变切换。
基于强化学习的PID伺服系统控制策略
基于强化学习的PID参数整定策略
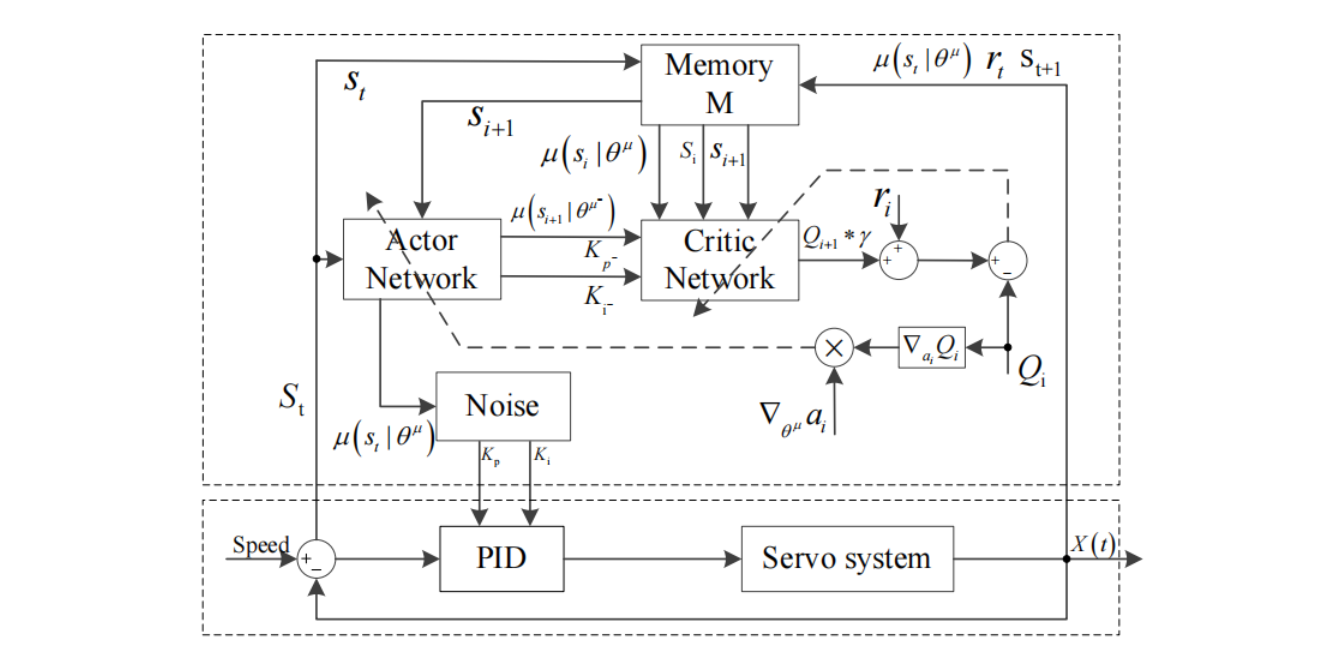
这篇文章首先使用actor-critic构建强化学习智能体1的框架,以PID伺服系统作为其环境对象。获得激励函数的跟踪误差曲线。采用确定性策略梯度算法设计动作网络,采用DQN算法设计评估网络。最终实现PID参数自整定。由于,前面将伺服系统的模型建立为PI控制,因此这里强化学习智能体的动作变量只有两个,分别是比例系数和积分系数。奖励函数由伺服系统输出角度的跟踪误差的绝对值构成。
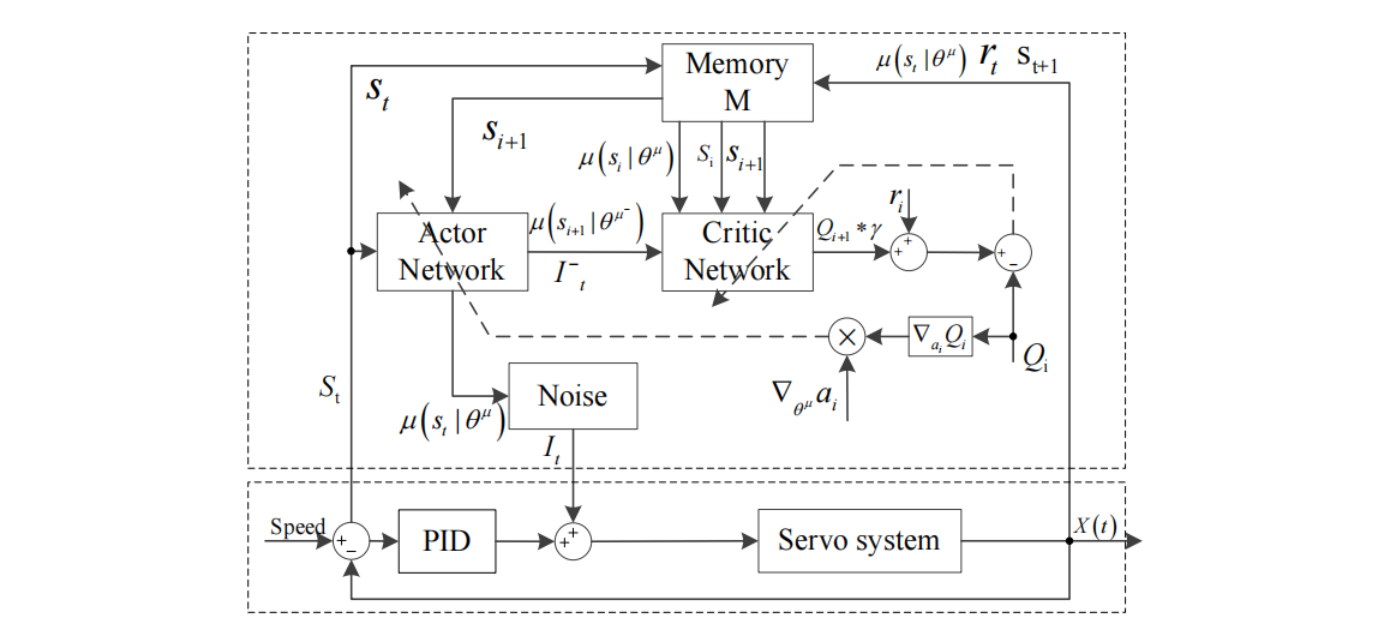
基于强化学习的自适应PID电流补偿策略
自适应PID电流补偿智能体2采用与智能体1相同的控制结构和算法,实现PID输出电流的自适应补偿。
实验结果
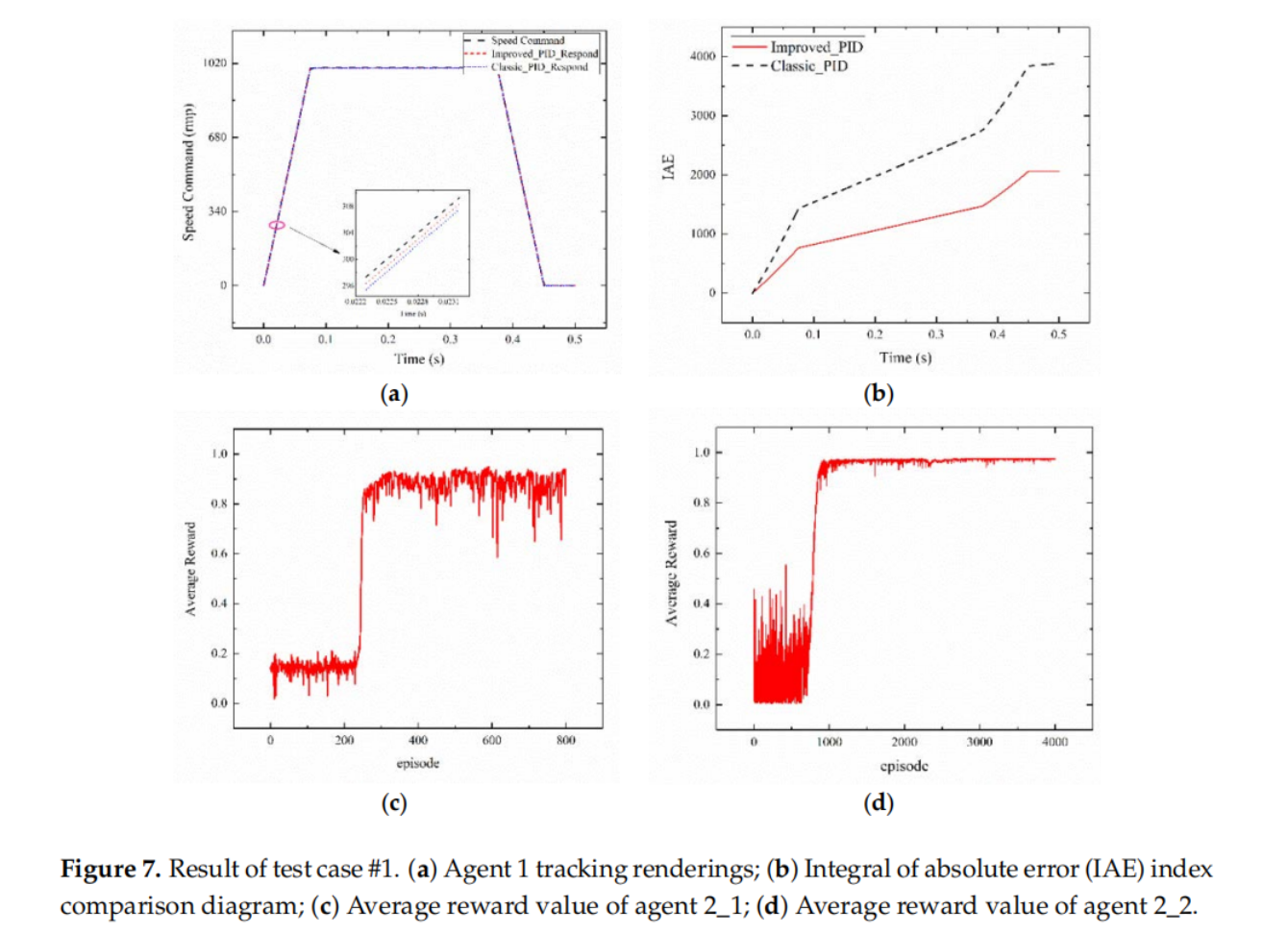
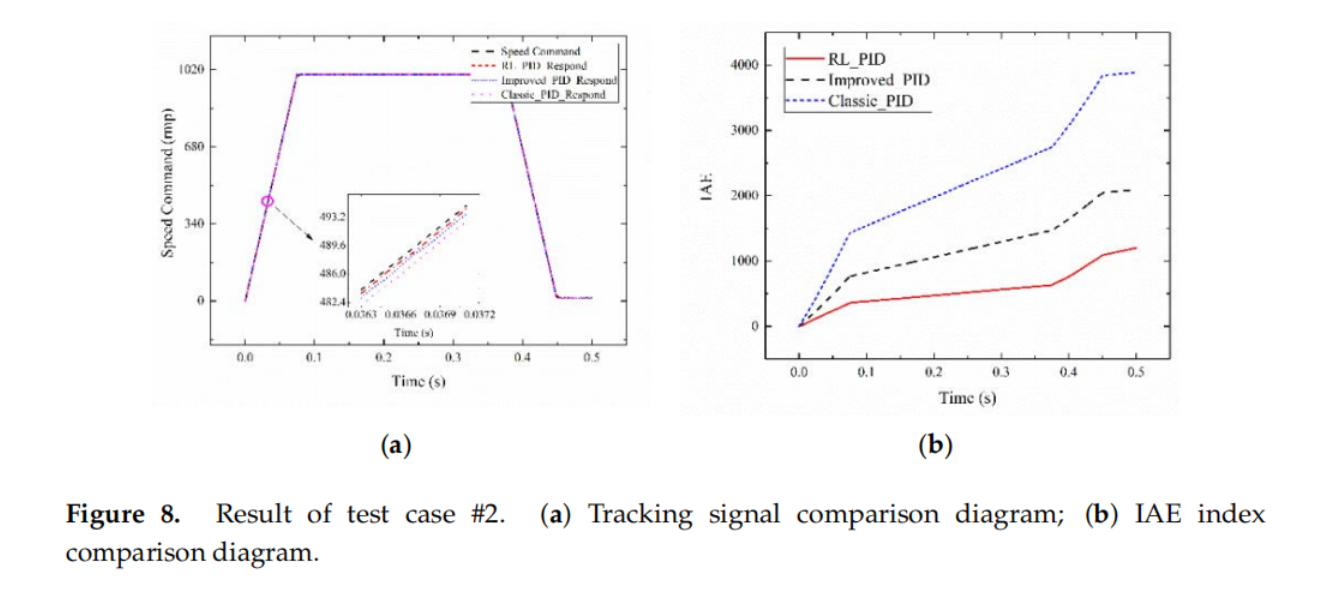
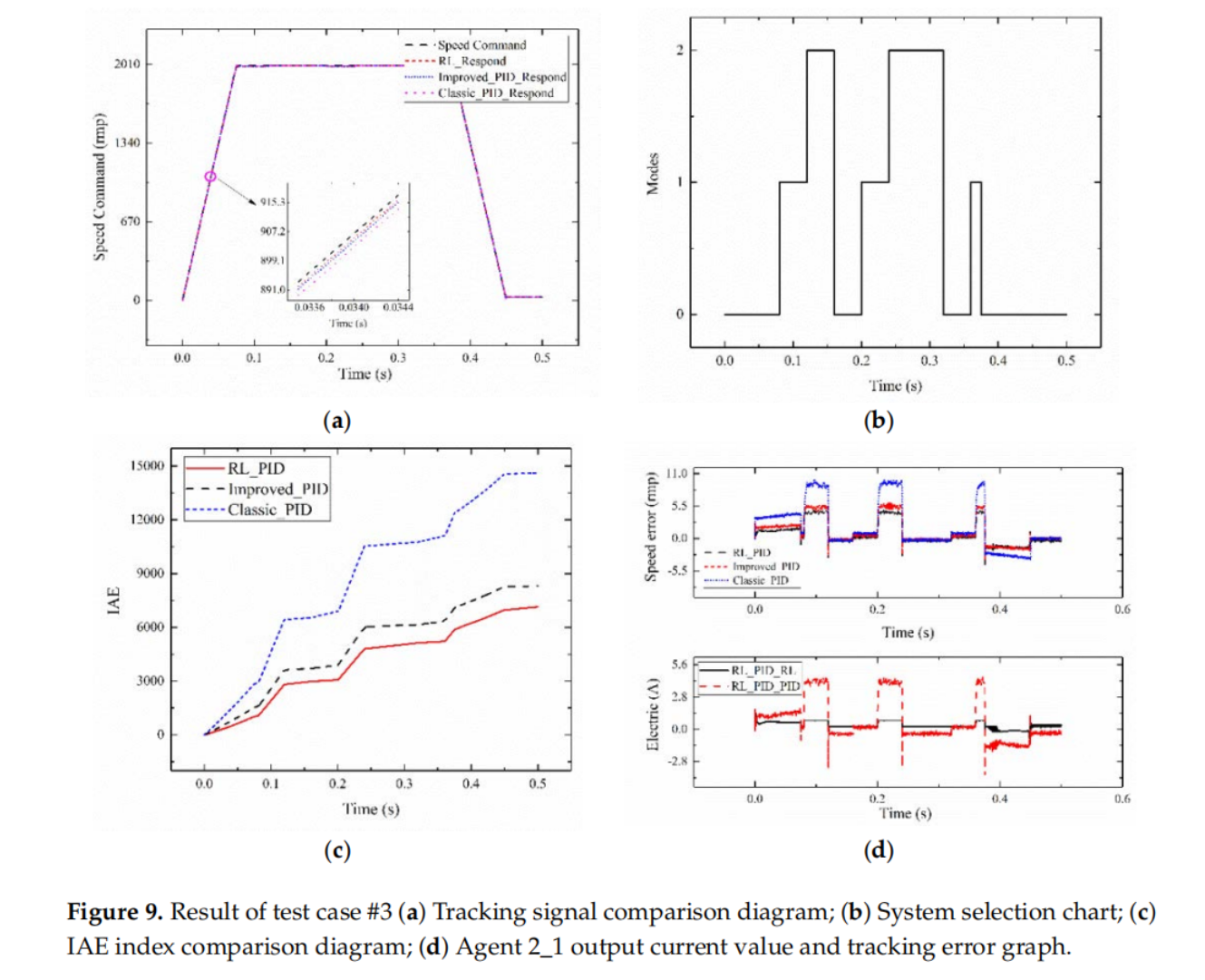
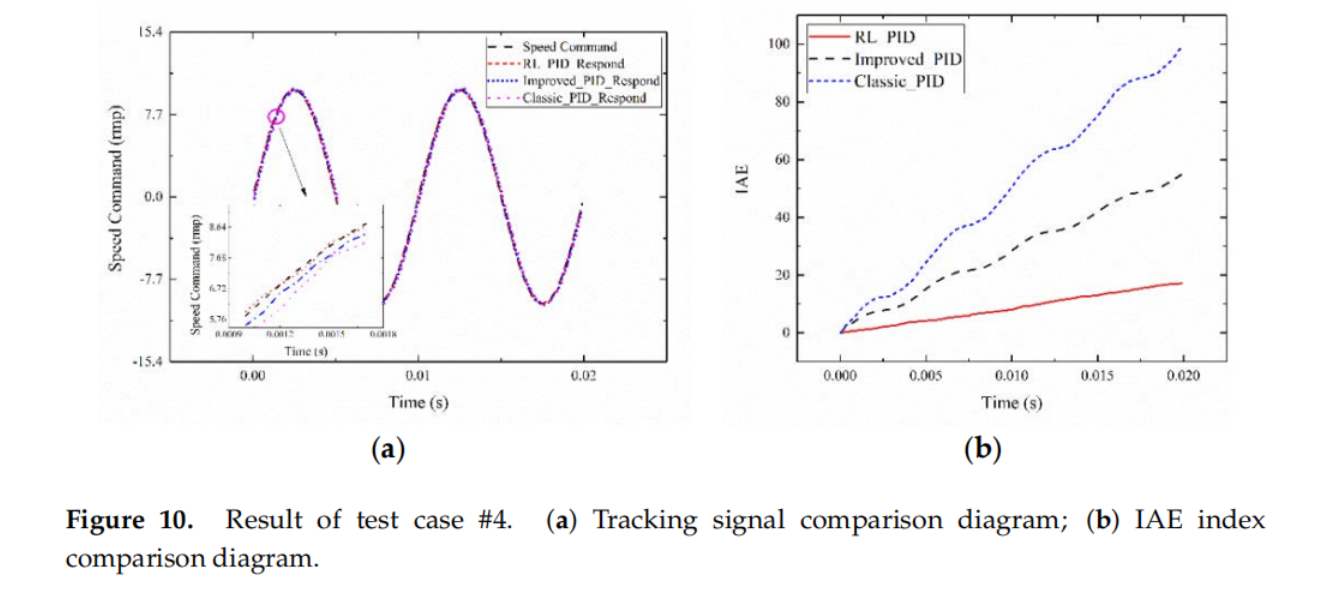
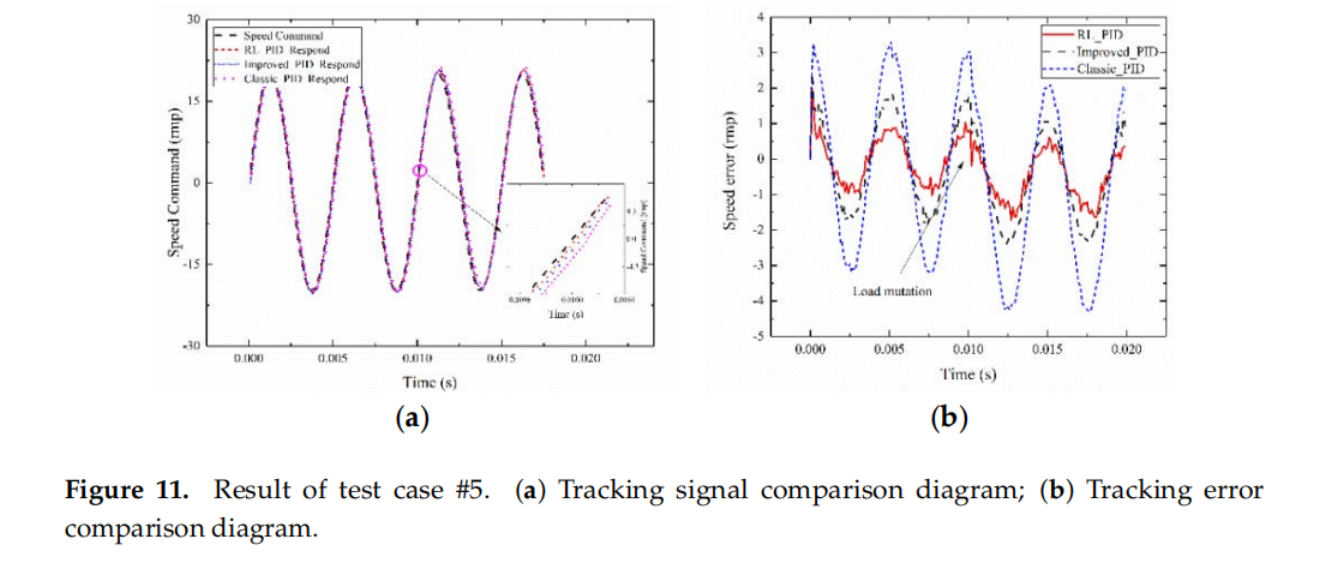
详细的实验配置和整体的实验结果可以参看论文原文,这里主要对几个重要的性能结果曲线图进行展示,可以看出利用强化学习不仅可以使伺服系统的控制参数进行快速、准确的整定,而且可以根据伺服系统的状态进行电流在线补偿,从而使得该系统能够有效克服外界因素的影响。