Rewrite the Stars
资源信息
主要贡献
论文揭示了star operation(元素乘法)在无需加宽网络下,将输入映射到高维非线性特征空间的能力。基于此提出了StarNet,在紧凑的网络结构和较低的能耗下展示了令人印象深刻的性能和低延迟。最近,通过元素乘法融合不同的子空间特征的学习范式越来越受到关注,论文将这种范例称为star operation(由于元素乘法符号类似于星形)。
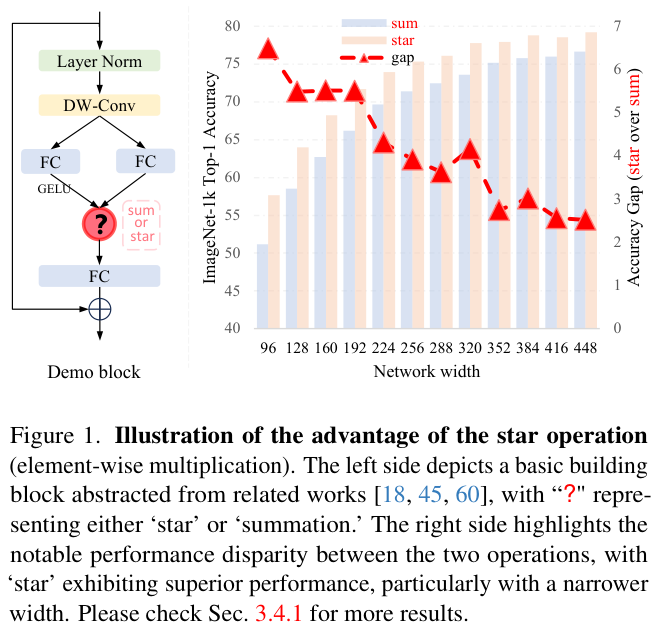
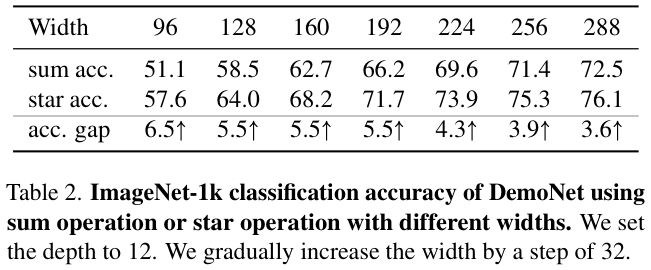
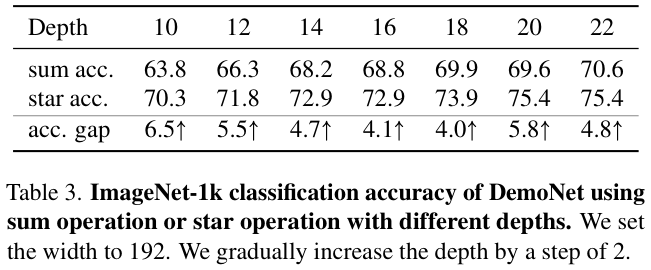
为了便于说明,论文构建了一个用于图像分类的demo block,如图 1 左侧所示。通过在stem层后堆叠多个demo block,论文构建了一个名为DemoNet的简单模型。保持所有其他因素不变,论文观察到逐元素乘法(star operation)在性能上始终优于求和,如图 1 右侧所示。
在这项工作中,论文证明star operation具有将输入映射到极高维的非线性特征空间的能力,从而解释star operation的强表达能力。论文不依赖直观或假设的高级解释,而是深入研究star operation的细节。通过重写和重新表述star operation计算过程,论文发现这个看似简单的运算实际可以生成一个新的特征空间,含大约 线性独立维度。
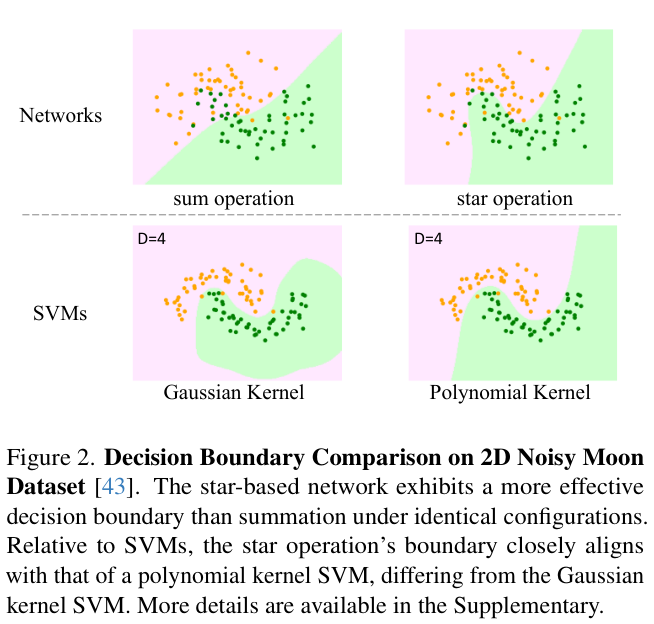
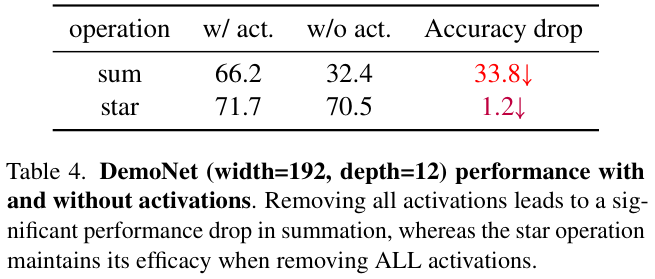
与增加网络宽度(又称通道数)的传统神经网络不同,star operation类似于在不同通道上进行成对特征乘法的核函数,特别是多项式核函数。当应用到神经网络中并通过多层堆叠时,每一层都会带来隐式维度复杂性的指数增长。只需几层,star operation就可以在紧凑的特征空间内实现几乎无限的维度。在紧凑的特征空间内计算,同时受益于隐含的高维度,这就是star operation的独特魅力所在。
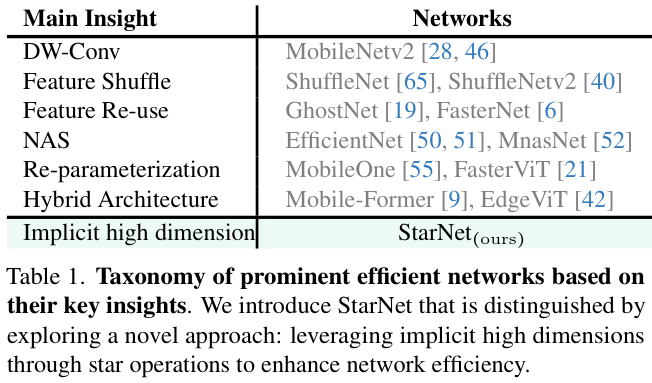
根据上述见解,论文推断star operation本质上更适合高效、紧凑的网络,而不是常规使用的大型模型。为了验证这一点,论文提出了一种概念验证的高效网络StarNet,其特点是简洁和高效。StarNet非常简单,缺乏复杂的设计和微调的超参数。在设计理念上,StarNet与现有网络明显不同,如表 1 所示。利用star operation,StarNet甚至可以超越各种精心设计的高效模型,如MobileNetv3、EdgeViT、FasterNet等。这些结果不仅从经验上验证了论文对恒星运行的见解,而且强调了其在实际应用中的实用价值。
论文简要总结并强调这项工作的主要贡献如下:
- 证明了star operation的有效性,如图 1 所示,揭示了star operation具有将特征投影到极高维隐式特征空间的能力,类似于多项式核函数。
- 从分析中汲取灵感,确定了star operation在高效网络领域的实用性,并提出了概念验证模型StarNet。无需复杂的设计或精心选择的超参数即可实现高性能,超越了许多高效的设计。
- 基于star operation存在大量未探索的可能性,论文的分析可以作为指导框架,引导研究人员远离随意的网络设计尝试。
鉴于star operation的独特优势—在低维空间中计算的同时产生高维特征,论文确定了其在高效网络架构领域的实用性。因此,论文提出StarNet作为概念验证模型,特点是极其简约的设计和显著减少的人为干预。尽管StarNet很简单,但它展示了卓越的性能,强调了star operation的功效。
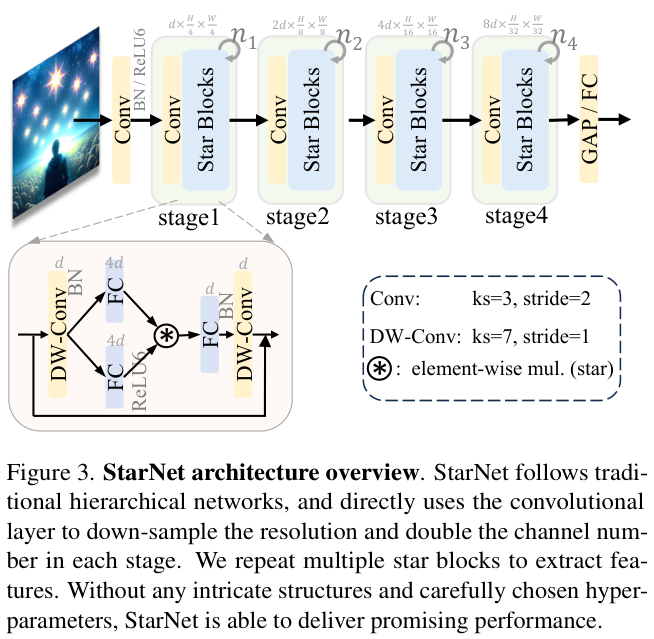
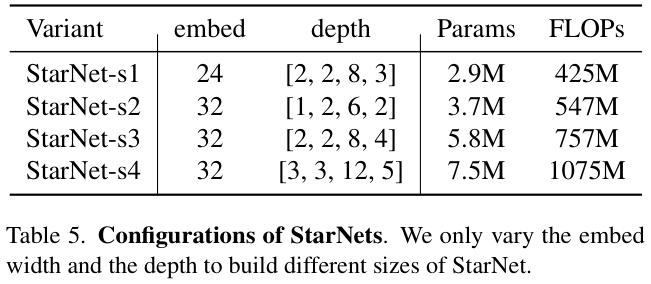
StarNet采用 4 级分层架构,利用卷积层进行下采样,并使用修改后的demo block进行特征提取。为了满足效率的要求,将Layer Normalization替换为Batch Normalization,并将其放置在深度卷积之后(可以在推理时融合)。受到MobileNeXt的启发,论文在每个块的末尾加入了一个深度卷积。通道扩展因子始终设置为 4,网络宽度在每个阶段加倍。遵循MobileNetv2设计,demo block中的GELU激活被替换为ReLU6。
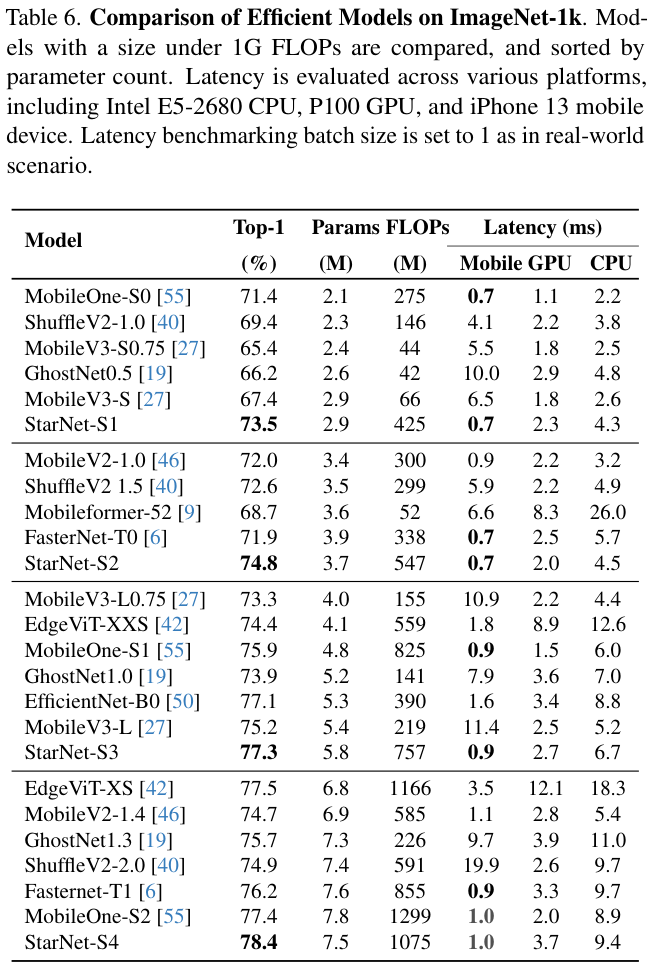
实验结果